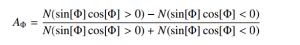REDTOP experiment

Why an experiment based on the η and η’ mesons

The η meson is a very special particle, indeed. First of all, the η is a Goldstone boson, therefore symmetry constrains its QCD dynamics. There aren’t many Goldstone bosons in nature: among those, the η meson is even more special since it is an eigenstate of the C, P, CP and G operators (very rare in nature): I^GJ^PC=0⁺0^-+. An immediate consequence of the latter is that it can be used to test C and CP invariance.  It is worth noticing that the η quantum numbers are the same as the vacuum, except for its parity which is the opposite. The fact that all its additive quantum numbers are zero makes the η meson especially useful when looking for symmetry violating decays, since there are no flavor changing currents that would influence the processes in an unknown way. This is quite an opposite situation of the symmetry violating processes of the K and B meson families, mostly used in the past for studying the physics beyond the Standard Model, where either the strangeness or the beauty flavor has to disappear. Instead, the η decays are all flavor-conserving  reactions.

Another interesting aspect of the η dynamics is that all its possible strong decays are forbidden in lowest order by P and CP invariance, G-parity conservation and isospin and charge symmetry invariance. Similarly, electromagnetic decays are forbidden in lowest order by C invariance and angular momentum conservation. There are two consequences of the above properties:

• the η is a very narrow state (Γ_η=1.3 KeV vs Γ_ρ=149 MeV, for example) . This helps considerably in reconstructing the final state since the invariant mass of the latter has to match the η mass;
• the contributions from higher-order processes  are enhanced by a factor of ~100,000. Therefore η decays are mostly free of Standard Model backgrounds for new physics search.

Summing up the η meson is an excellent laboratory for searching for physics beyond the Standard Model, provided that an experiment could be designed to produce in excess of 10¹³ such particles. REDTOP is being designed to do exactly this with a detector highly sensitive to processes from new physics, but mostly insensitive to background from old physics.

We list below the physics processes that REDTOP intends to study.

CP Violation (Type I: P and T odd, C even)

There are two ways of violating the CP operator: the first is when the parity of the final state is reversed, but its charge conjugation is not. This situation occurs when the P=-1 η meson decays into an even number of pions. In hadro-production experiments as is the case for REDTOP, trying to disentangle two pions from the η decay is virtually impossible. Therefore, the final state of interest for this studying this class of CP violation is:

η → 4π^o → 8γ         

which occurs when the P=-1 η meson decays into an even number of pions.

CP Violation (Type II: C and T odd , P even)

The second way of violating the CP operator is when the charge of the final state is reversed, but its parity is not. This occurs, for example, in the following class of decays:

η → π^o l⁺ l^–          and             η → 3γ 

The decay η → π^ol⁺l^–  violates C (and CP) if it occurs via a single photon intermediate state. The two photon intermediate state is, on the other hand, allowed within the Standard Model with an α⁴  coupling and an expected branching ratio of the order of 10^-8. By comparing the branching ratios of η → π^ol⁺l^–  and  η → 3γ one could, eventually, disentangle the CP violating contribution from the CP conserving one. This would be a new kind of CP violation, which is also a C violation. It could solve the cosmological problem of the known baryon excess over anti-baryons by ten orders of magnitude. 

The known CP violation in K^o decay is not sufficient for this purpose. It could also explain a peculiar asymmetry of the Standard Model, namely, that the basic constituents of that model are left­ handed doublets and right­-handed singlets quarks and leptons.

CP Violation via the polarization of the muons

CP invariance does not allow the muons in:

η → μ⁺μ^–

to be longitudinally polarized. Any polarization requires a CP violating lepton-quark current. Since in the minimal Standard model the polarization of the muons is not observable, an immediate implication of observing a non-zero longitudinal polarization of the muons is the existence of an extra Higgs boson. If that is the case, then the muon polarization would be as high as 10^-2.

CP and C Violation with Dalitz plot studies

CP invariance requires that in the following decay of the η meson:

η → π⁺π^–π^o

the dynamics of the charged pions are totally symmetric. Consequently, the Dalitz plot of that decay should show no signs of asymmetries. On the contrary, any mirror-asymmetry in the Dalitz plot would be an indication of CP and C violation. Such asymmetry does not arise from SM operators at tree level, nor can the operators that generate EDMs contribute to it (at tree level). Consequently, the violation of discrete symmetry resulting from studing this process  is not bounded by EDM as is the case for the η→4π  process. Furthermore, this  measurement is complementary to EDM searches even in the case of T and P odd observables, since the flavor structure of the eta is different from the nucleus (S. Gardner). See, also, this presentation by S. Gardner for more insights on this topic.

CP Violation with gamma polarization measurements or in η → π⁺π^–e⁺e^– decays

In principle one could investigate CP violation by looking at E1 transitions of the photon in the decay η → π⁺π^– γ This would require that the photon polarization, which is measured with a gamma polarimetr. At present, such a subdetector is, at present,  considered optional in REDTOP apparatus. An other possible way to probe the CP-violation is when the photon is virtual and it decays decaying into a e⁺ e^– pair:

η → π⁺π^–γ^* with γ^* → e⁺ + e^–

CP invariance requires that in the following asymmetry

is vanishing (Φ is the angle between the decay planes of the electron-positron pair and the two charged pions).

The best present measurement of such asymmetry has been performed bt the WASA collaboration ( P. Adlarson et al., arXiv:1509.06588 [nucl-ex]) and it is consistent with zero within the measurement errors. However, the statistical error (based on the production of ∼ 10⁹ η-mesons) largely dominates that measurement. REDTOP larger statistics will improve on the systematic error by almost two orders of magnitude, bringing the sensitivity to a level  where CP-violation could be observed.

The proton radius anomaly

The processes involved are:

η → γ e⁺e^–       and         η →γ μ⁺μ^–

One of the existing and still unexplained anomaly present in the Standard Model is related to the measurements of the proton radius – R_p – with electron and muon probes. Experiments measuring R_p by investigation of the levels of muonic atoms (see, for example, CODATA-2012) or by elastic scattering of electrons and muons on hydrogen atoms are finding a discrepancy of several sigma in the electron vs muon case. Those processes occur mainly trough the exchange of one virtual photon. On the other side, processes like η → γ l⁺ l^–  can occur either via one photon (diagram a)) or two photons (diagram b)).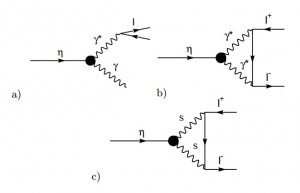

However, the existence of a light scalar particle S which couples differently to electrons and muons, could mediate the process via the diagram c). Consequently, a precise measurement of the branching ratios of the latter might help in explaining the R_p anomaly.

Search for true muonium

True muonium is a bound state of a μ +μ – pair with a well defined mass of about 2M_μ [1]. It is expected to decay into a e⁺e^–   pair with a large branching ratio. The processes involved are:

η →γ (μ⁺μ^– )|_2Mμ→ γ e⁺e^–  

This state has not been observed yet. Detection of true muonium would be an important discovery and would represent a further important test of QED. If the branching ratio of η decaying into true muoniom is larger than about 10^-9, it will be relatively easy to observe since REDTOP targets are very thin (< 240 mm) and the electron positron pairs in the final state will leave the nuclear matter mostly undisturbed.

T Violation via the polarization of the muons

T invariance requires a null transverse polarization of the muons in:

η → π^oμ⁺μ^–       and         η →γ μ⁺μ^–

Any observed polarization is a direct violation of T invariance.

CPT Violation

CPT invariance can be probed with the following two processes:

η → π⁺μ^–ν        vs      η →π^–μ⁺ν

If CPT holds, then we expect that the transverse polarization of the μ^– and that of the μ+ be reversed. Namely, PT(μ⁺) = -PT (μ^–). As an aside note,  the η → πμν  has not been observed yet.

CPT Violation with non-hermitian lagrangians

CPT invariance and hermiticity of the lagrangian implies that in the following processes:

η → γγ     and   π^o → γγ

the photons have  null circular polarization. Although we believe that the lagrangians for physical processes have to be Hermitian, L. B. Okun has a strong argument for which that has not necessarily be the case [2]. Of course, the observation of a non-null circular polarization of the photons is an indication of CPT violation and of non-hermiticity of the lagrangian as well.

Lepton flavor violation

Violation of the leptonic number will be observed through the following process:

η → μ⁺ e^–  + c.c.      and    η → π^o μ⁺ e^–  + c.c.

Current PDG limits are <5.7 x10^-13, CL=90%  (from the direct muon decay μ^– → e^–γ). REDTOP will have a lower sensitivity (one order of magnitude). However, the process involved and the experimental technique are different and it is worth to explore it.

Double lepton flavor violation

Double violation of the leptonic number will be observed through the following process:

η → μ⁺ μ⁺ e^–  e^–    + c.c.

This is expected a very rare process to occur. Nonetheless, it it occurs within the sensitivity of the experiment, it will be easily detected has it carries a very unique signature.

Direct searches for dark photons

The dark (or, sometimes, heavy) photon A’ is a U(1) vector boson , mediator of a possible new force.  From the astrophysical observations of several anomalies the mass of such particle is expected to be in the GeV-scale. If it is below the mass of the η meson it can be observed via the following processes:

η → γ A’ → γ + l⁺l^– 

From the experimental point of view, the two η and A’ mass constraints will help to reject the background. Therefore, the search for dark photons at Fermilab will complement the similar searches by the new experiments at Jefferson Lab and Frascati with g and e^– beams.

Indirect searches for dark photons and new gauge bosons

The existence of such a dark photon with mass of the order of the  GeV would affect the value of the branching ratios for the decay:

η → e⁺e^–

The Standard Model predicts such branching ratio to be of the order of about 10^-9. This is because the process occurs through an intermediate state with two virtual photons. Consequently, it is suppressed with respect to the η → γγ decay by a factor α² and the mass ratio (me/mη) ². The low probability of this process makes it sensitive to the new forces that would contribute through the presence of extra loops. It is intriguing that a similar measurement performed by KTev on the π^o meson has revealed a discrepancy with the Standard Model predictions by 3.3σ (E. Abouzaid et al. Phys. Rev. D75 (2007) 012004), indicating a possible contribution by new physics. The decay of the  η meson into an electron and a positron pair has never been observed experimentally, with the best upper limit set by the WASA-at-COSY experiment BR(η → e +e −) < 4.5×10^-6 at 90% CL (arXiv:1406.5738).  From the experimental point of view, the η  mass constraints will help to reject the combinatorics background from electrons and positron generated by gamma conversion in the beam pipe.

Searches for new baryonic forces

This is a similar search as for the dark photon case, but without the mass constraint on the resonance. If the vector boson B mediating that force is below the mass of the η meson it can be observed via the following processes:

η → γ B  with B → γπ^o                and           η → γ B  with B → γ + l⁺l^– 

New forces in the MeV-GeV range associated with dark matter are postulated by several models; some of them are listed below:

• Sommerfeld-enhancement models of Dark Matter and indirect detection anomalies (ex. Pamela) – Pospelov and Ritz (2008), Arkani-Hamed, et al (2008)
• Self interacting Dark Matter and explaining small scale structure anomalies in dwarf galaxies – Feng, et al (2009), Loeb and Weiner (2010), S. Tulin, Yu, Zurek (2013)
• Asymmetric Dark Matter models – Lin, et al (2011)
• Hidden sector DM and relic density – Feng, et al (2009)

Searches for leptoquarks

Leptoquarks are particles mediating a new interaction between quarks and leptons of the same generation. They are color-triplet bosons that carry both lepton and baryon numbers. REDTOP would observe their effects in the following process:

η → μ⁺μ^–    and    η → e⁺e^–

Any discrepancy between the rate observed and predicted by the Standard Model would be an indication of additional contributions from new diagrams. Leptoquarks are present in various extensions of the Standard Model, for example technicolor theories or some GUTs based on Pati–Salam model, SU(5) or E6.

Searches for new scalar particles – dark Higgs

The final state to be studied is:

η → π^o H  with H →  e⁺e^–  and μ⁺μ^–    

This process can only occur in the Standard Model via a two-photon exchange diagram with a branching ratio of the order of 10^-9. The existence of a light scalar particle coupling the muons to the quarks will change the dynamics of the process by increasing its probability of occurrence even by several orders of magnitude. REDTOP’s expected sensitivity is greater that 10^-10 for this channel, good enough to be able to shed some light onto the underlying physics. Furthermore, a precision measurement of the branching ratio, along with unitarity constraints and with the measurements from η -> π^o γγ  will reveal if there is any “abnormality” in the two photon channel. It will also provide strong constraints on new physics models where a light new particle mediates interactions. In particular, improving the limit on this branching ratio would restrict the parameter space of models “designed” to explain the R_p discrepancy.  In such models, the coupling to quarks would have to break isospin because one wants to avoid couplings to neutrons (M. Pospelov).

 

Searches for ALPS

Axion-Like Particles (ALPS) are extensions of the QCD axions postulated long ago to fix, among other things, the Strong CP Problem . They could be obtained from the decay of the h or h’ mesons according to the following process:

η → π^– π⁺ a   or    η → π^oπ^o a 

ALPS are pseudoscalar particles coupling to photons. Depending on the underlying theory model, they can decay preferably into  γγ, leptons or quarks.  REDTOP’s expected sensitivity depends on the underlying model, reaching values of g_Y (the coupling parameter of ALPS to leptons) of the order of  10^-8 .

 

Non-η searches: Drell-Yan production of a dark photon

Since the dark photon couple to ordinary matter trough a regular photon, it can be generated when an intense proton beam hits one of the Be targets inside REDTOP. The process would be a Drell-Yan scattering:

q qbar → A’   → l⁺l^– 

REDTOP will have more than 10¹⁸ protons on target (POT) and the detached vertex of the di-lepton system, in addition to a bump in the invariant mass of the latter, would be able spot a dark photon among QCD background.

 

Non-η searches:  production of a ALPS from quark-antiquark scattering

Since an ALP couples to photons and, in some models, also directly to quarks, it could be produced from the scattering of an intense proton beam onto a thin target.:

q qbar → ALP + X   

Depending on the underlying theory model, they can decay preferably into  γγ, leptons or quarks.  REDTOP’s expected sensitivity depends on the underlying model, reaching values of g_G (the coupling parameter of ALPS to quarks) of the order of  10^-7 for masses of the ALP ranging from about 15 MeV up to about 2 GeV.

Non-η searches: π^o decays

A π^o  could decay into a dark photon trough the following process:

π^o  →γ   A’  →γ γ γ

About 10¹⁵ /year π^o ‘s  will be produced on the target systems of REDOP. A bump in the invariant mass of two photons, is a signature to reveal a dark photon among the continuous QCD background.

Another important process to study would be:

π^o  →e⁺e^–

The KTev has determined that BR( π^o → e +e −) = ( 6.44 ± 0.25 ± 0.22 ) 10^-8, indicating a discrepancy with the Standard Model predictions by 3.3σ (E. Abouzaid et al. Phys. Rev. D75 (2007) 012004). A measurement by REDTOP based on a larger statistical sample and with a detector covering a larger solid angle will be able to confirm or reject that discrepancy, which could be, in fact, a hint of new physics.

Non-η searches: π⁺ and kaon decays

A π+  or a charged kaon could emit  a dark photon trough one of the following rare process:

π⁺ → μ^–ν A’   → μ^–ν e⁺e^–  and  K⁺ → μ^–ν A’   → μ^–ν e⁺e^–  

More tha 10¹⁵ /year π+ ‘s  will be produced on the target systems of REDOP while the charged kaons will be produced only when running at the  η’. A bump in the invariant mass of e⁺e^–  systems and a detached vertex betwuen the muon and the e⁺e^– pair will be a clear signature to reveal a dark photon among the continuous QCD background. See, also, C.W. Chiang and P. Y. Tseng, 2016 [arXiv:1612.06985v1].

High precision studies on physics beyond the Standard Model

Generally, new limits on discrete symmetry breaking in eta decay constrain the low-energy constants associated with BSM operators. Improving the eta decay limits sets constraints on the energy scale at which such operators can appear. These are complementary to EDM searches even in the case of T and P odd observables, since the flavor structure of the η is different from the neutron (S. Gardner). REDTOP is designed as an hermetic and high precision experiment where the η decays can be observed with excellent sensitivity. In fact, all the branching ratios accessible will be either observed for the first time or measured with good accuracy. Consequently, REDTOP will most likely shed some new light on physics beyond the standard model and on several models being proposed so far.

Nuclear and intermediate-energy physics

Given its peculiarities, the η meson has been traditionally used to study low and intermediate energy physics. A list of possible topics that fall in those categories is:

• Nuclear models
• Chiral perturbation theory
• Non-perturbative QCD
• Isospin breaking due to the u-d quark mass difference
• Octet-singlet mixing angle
• ππ interactions
• Electromagnetic transition form-factors (important input for g-2)

The two most important such measurements would be:

• a determination of two low energy constants present in chiral perturbation theory at order p⁶ from η → π^oγγ decay;
• a very high statistics determination of the light quark mass ratio Q from η → 3π decays.

The large number of η mesons produced (which is about 100,000 times the entire existing event sample) would make all those studies even more precise and it will allow to explore new, more rare processes.

 

References

1. S. J. Brodsky and Richard F. Lebed, PRL 102, 213401 (2009)

2. L. B. Okun, arXiv:hep-ph/0210052.